十大排序算法复习

本文最后更新于：2024年8月5日 下午

十大排序算法

  • 由于面试/笔试中，排序算法是常见的考察内容，特于此系统性复习一下

排序算法可以分为内部排序和外部排序。

内部排序是数据记录在内存中进行排序。

而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

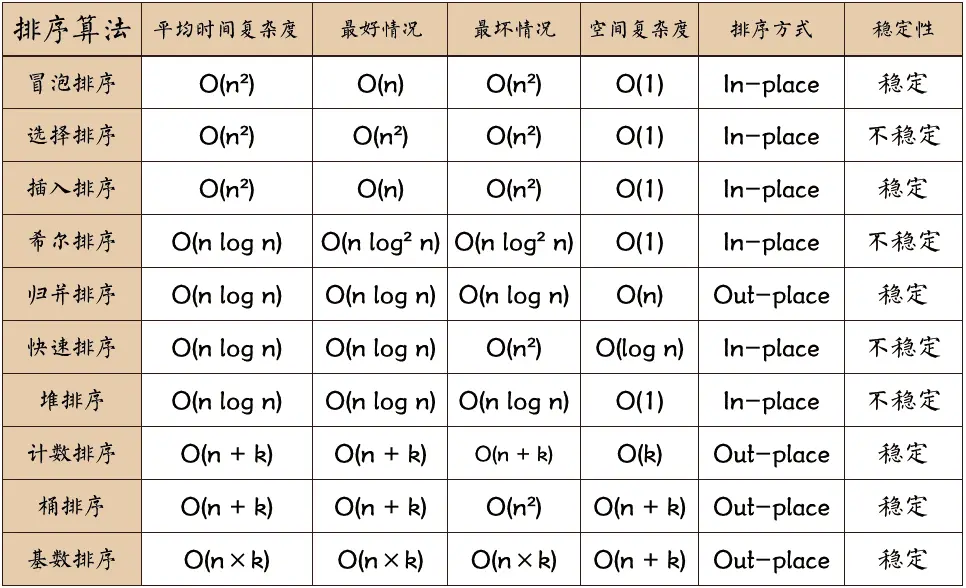
常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

关于时间复杂度：

  1. 平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。
  2. 线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；
  3. O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序
  4. 线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性：

  1. 稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。
  2. 不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

冒泡排序

  • 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  • 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
  • 针对所有的元素重复以上的步骤，除了最后一个。
  • 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

选择排序

  • 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
  • 再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
  • 重复第二步，直到所有元素均排序完毕。

插入排序

  • 将待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
  • 从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

希尔排序

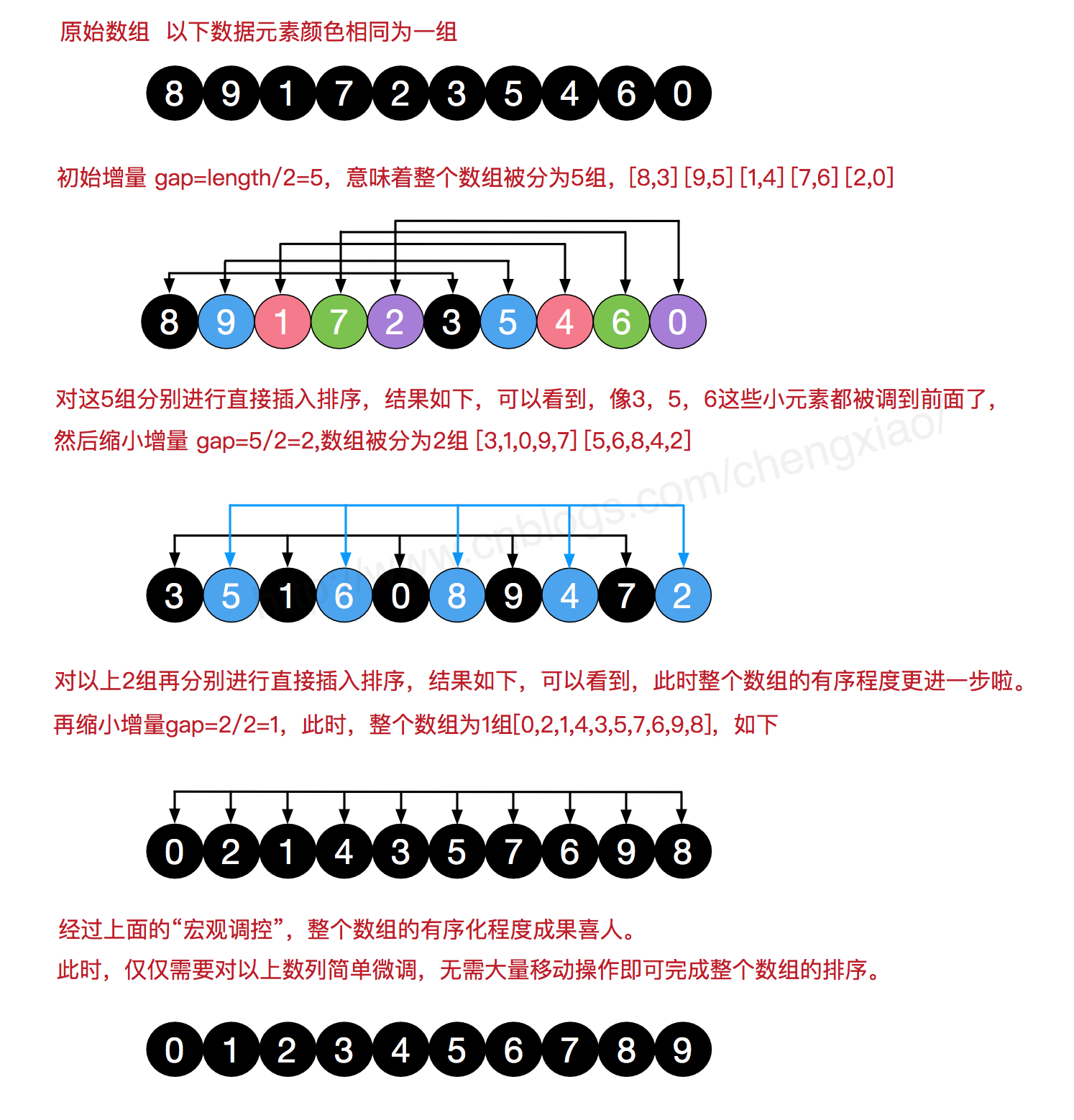
  • 跳跃地进行分组，组内进行插入排序；
  • 将分组间隔减小，继续进行插入排序；
  • 当所有数据为1组时，进行最后的插入排序，此时只需要少量操作就能完成；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include<iostream>
using namespace std;

//希尔排序

void sort_shell(int arr[], int len)
{
	for (int gap = len / 2; gap >= 1; gap /= 2)
	{
		//cout << "gap = " << gap << endl;
		for (int j = gap; j < len; j++)
		{
			for (auto i = 0 ; i < len ; i++)
			{
				cout << arr[i] << " ";
			}
			cout << endl;
			int k = j - gap;
			int tmp = arr[j];
			while (k >= 0 && arr[k] > arr[j])//移动法进行插入排序
			{
				arr[k + gap] = arr[k];
				k -= gap;
			}
			arr[k + gap] = tmp;
		}
	}
}

int main()
{
	int arr[10] = { 1 , 233, 42, 24, 20, 87, 12, 856, 23, 67 };
	sort_shell(arr, 10);
	for (auto i : arr)
	{
		cout << i << " ";
	}
	cout << endl;
	return 0;
}

归并排序

  • 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
  • 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
  • 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
  • 重复步骤 3 直到某一指针达到序列尾；
  • 将另一序列剩下的所有元素直接复制到合并序列尾。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include<iostream>
using namespace std;

//归并排序

void static merge_dc(int* arr, int left, int right, int* tmp)//对已经排序好的两个数组进行归并
{
	int mid = (left + right) / 2;
	int t = 0;
	int t_left = left;
	int t_right = mid + 1;
	while (t_left <= mid && t_right <= right)
	{
		if (arr[t_left] < arr[t_right])
		{
			tmp[t++] = arr[t_left++];
		}
		else
		{
			tmp[t++] = arr[t_right++];
		}
	}
	if (t_left == mid + 1)
	{
		while (t_right <= right)
		{
			tmp[t++] = arr[t_right++];
		}
	}
	else if (t_right == right + 1)
	{
		while (t_left <= mid)
		{
			tmp[t++] = arr[t_left++];
		}
	}
	t = 0;
	while (left <= right)
	{
		arr[left++] = tmp[t++];
	}
}

void sort_dc(int* arr, int left, int right, int* tmp)//进行分治，将数组分为前后两个看待，分别排序
{
	if (left < right) {
		int mid = (left + right) / 2;
		sort_dc(arr, left, mid, tmp);
		sort_dc(arr, mid + 1, right, tmp);
		merge_dc(arr, left, right, tmp);
	}
}

void sort_dc(int arr[], int len)//一次性申请一块空间，避免递归过程中反复开辟、删除
{
	int* tmp_arr = new int[len];
	sort_dc(arr, 0, len - 1, tmp_arr);
	delete[] tmp_arr;
}


int main()
{
	int arr[11] = { 1,233, 42, 24, 20, 87, 12, 856, 23, 67 ,55};
	sort_dc(arr, 11);
	for (auto i : arr)
	{
		cout << i << " ";
	}
	cout << endl;
	return 0;
}


快速排序

  • 从数列中挑出一个元素，称为 “基准”（pivot）;
  • 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
  • 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<iostream>
using namespace std;

//quick排序

int Partiton(int* arr, int left, int right)
{
	int index = left;
	int pivot = arr[index];
	while (left < right)
	{
		while (arr[right] >= pivot && left < right)
		{
			right--;
		}
		arr[left] = arr[right];
		while (arr[left] <= pivot && left < right)
		{
			left++;
		}
		arr[right] = arr[left];
	}
	arr[left] = pivot;
	return left;
}

void Quick_Sort(int* arr, int left, int right)
{
	if (left >= right)	return;
	int p = Partiton(arr, left, right);
	Quick_Sort(arr, left, p - 1);
	Quick_Sort(arr, p + 1, right);
}

int main()
{
	int arr[5] = {-1,0,0,0,1};
	Quick_Sort(arr, 0, 4);
	for (auto i : arr)
	{
		cout << i << " ";
	}
	cout << endl;
	return 0;
}


堆排序

  • 创建一个堆 H[0……n-1]；
  • 把堆首（最大值）和堆尾互换；
  • 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
  • 重复步骤 2，直到堆的尺寸为 1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<iostream>
using namespace std;

//heap排序

void heapify(int* arr, int i, int len)
{
	int left = 2 * i + 1;
	int right = 2 * i + 2;
	int largest = i;
	if (left < len && arr[left] > arr[largest])
	{
		largest = left;
	}
	if (right < len && arr[right] > arr[largest])
	{
		largest = right;
	}
	if (largest != i)
	{
		int tmp = arr[largest];
		arr[largest] = arr[i];
		arr[i] = tmp;
		heapify(arr, largest, len);
	}
}


void buildheap(int* arr, int len)
{
	for (int i = len / 2; i >= 0; i--)
	{
		heapify(arr, i, len);
	}
}

void heapSort(int* arr, int len)
{
	buildheap(arr, len);
	for (int i = 0 ; i < len ; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;
	for (int i = 0; i < len; i++)
	{
		int tmp = arr[0];
		arr[0] = arr[len - i - 1];
		arr[len - i - 1] = tmp;
		heapify(arr, 0, len-i-1);
		for (int j = 0; j < len; j++)
		{
			cout << arr[j] << " ";
		}
		cout << endl;
	}
}

int main()
{
	int arr[11] = { 1,3, 42, 24, 20, 87, 12, 856, 23, 67 ,55};
	heapSort(arr,11);
	for (auto i : arr)
	{
		cout << i << " ";
	}
	cout << endl;
	return 0;
}


计数排序

  • 花O(n)的时间扫描一下整个序列 A，获取最小值 min 和最大值 max
  • 开辟一块新的空间创建新的数组 B，长度为 ( max - min + 1)
  • 数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
  • 最后输出目标整数序列，具体的逻辑是遍历数组 B，输出相应元素以及对应的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<iostream>
using namespace std;

//计数排序

void count_sort(int* arr, int len)
{
	int max = arr[0]; 
	int min = arr[0];
	for (int i = 0 ; i < len ; i++)
	{
		if (arr[i] > max)	max = arr[i];
		else if (arr[i] < min)	min = arr[i];
	}
	cout << "max:" << max << " min " << min << endl;
	int* tmp = new int[max - min + 1];
	for (int i = 0; i < max - min + 1; i++)
	{
		tmp[i] = 0;
	}
	for (int i = 0; i < len; i++)
	{
		tmp[arr[i] - min]++;
	}
	int index = 0;
	for (int i = 0; i < len; i++)
	{
		while (tmp[index] == 0)
		{
			index++;
		}
		if (tmp[index] > 0)
		{
			arr[i] = index+min;
			tmp[index]--;
		}	
	}

}


int main()
{
	int arr[11] = { 1,3, 42, 24, 20, 87, 12, 6, 23, 67 ,55};
	count_sort(arr,11);
	for (auto i : arr)
	{
		cout << i << " ";
	}
	cout << endl;
	return 0;
}


桶排序

  • 设置固定数量的空桶。
  • 把数据放到对应的桶中。
  • 对每个不为空的桶中数据进行排序。
  • 拼接不为空的桶中数据，得到结果

即，分割数据后，再对各个桶选取合适的排序算法。

例如将待排序的十个数，放入5个桶内，每个桶分别用快排。

基数排序

  • 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零
  • 从最低位开始，依次进行一次排序
  • 从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列

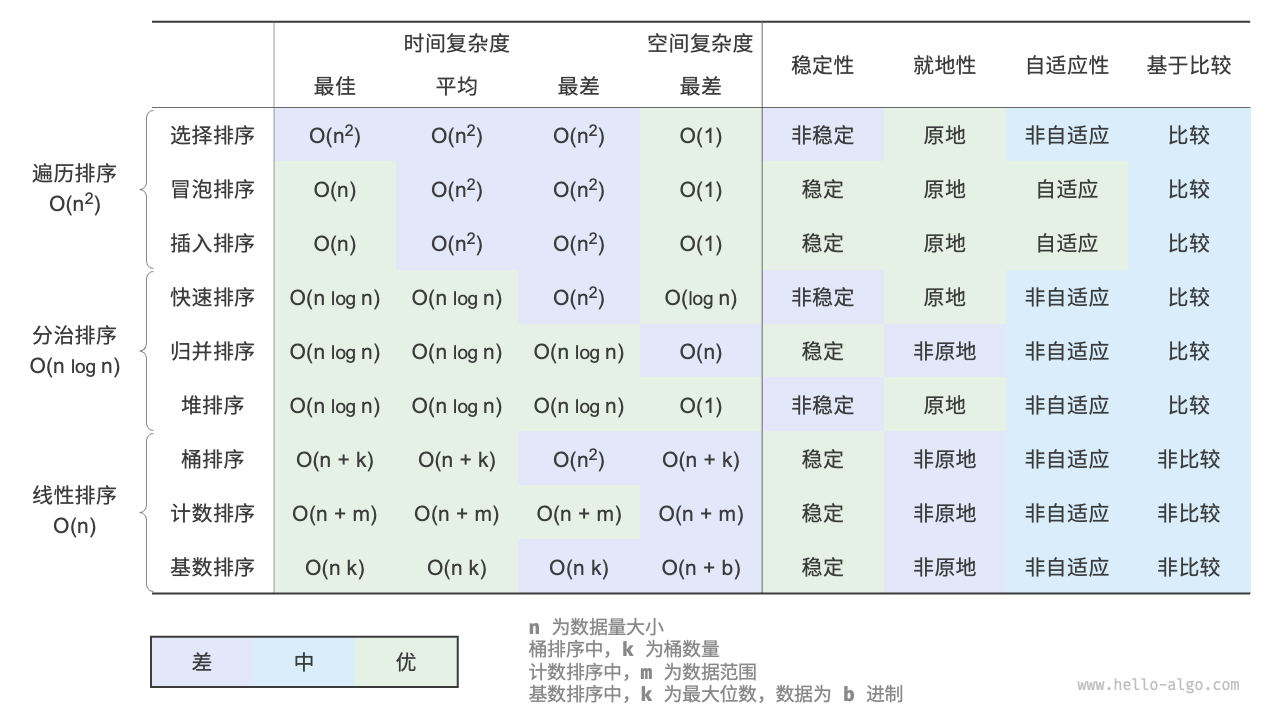
总结

排序算法对比

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！